Programación en C

ASIGNACIÓN DINÁMICA Y ESTRUCTURAS NO LINEALES

Introducción - Concepto de nodo .
Concepto de lista enlazada .
Inserción y eliminación de nodos

Introducción. Concepto de nodo.
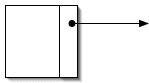
Los elementos de que constan las estructuras no lineales se conocen con el nombre de nodos. Un nodo es una estructura, con una particularidad: al menos uno de los campos de la estructura es un puntero de una estructura de ese mismo tipo. Esto es,la forma de un nodo es la siguiente:

struct Nodo {
 struct Nodo * puntero;
 /*
  Otros campos...
 */
};

Aunque pueda parecer una definición incorrecta, por ser recursiva, no lo es, porque el primer campo es un


						struct Nodo *

, que no es lo mismo que un


						struct Nodo

. Todos los punteros ocupan 4 bytes, así el "coste" adicional de un puntero suele ser una fracción pequeña del tamaño total del nodo.

Un ejemplo más real de nodo puede ser el siguiente:

struct Nodo {
 /* Campos de información */
 char modelo[10];
 int fecha;
 char fabricante[20];
 float peso;
 /* Campo de enlace */
 struct Nodo * sig;
};

Este nodo tiene como último campo un puntero llamado

sig

; como cabía esperar es un puntero de


						struct Nodo

. Obsérvese que los nodos no son otra cosa que registros de una base de datos dotados de uno o más punteros adicionales, destinados a crear estructuras de datos no lineales más flexibles que las tradicionales.

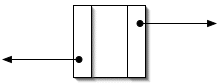
struct Nodo2 {
 /* Campos de información */
 char modelo[10];
 int fecha;
 char fabricante[20];
 float peso;
 /* Campos de enlace */
 struct Nodo * ant;
 struct Nodo * sig;
};

Otra posibilidad es dotar al nodo de dos punteros, en lugar de uno. Esto exige que la estructura asociada posea dos campos de enlace en lugar de uno; el coste de memoria sigue sin ser excesivo y supone ventajas importantes, como comprobará más adelante.
La estructura de la izquierda está dotada de los dos campos de enlace mencionados. Este tipo de nodo se emplea para construir listas doblemente enlazadas .

Los campos de enlace son la base de la construcción de estructuras dinámicas no lineales. Una de las estructuras no lineales más importantes es la lista enlazada, que se estudia a continuación.

Concepto de lista enlazada.
Las estructuras lineales se caracterizan porque sus elementos ocupan posiciones contiguas de memoria. La ventaja de esta distribución es la gran rapidez de acceso que permite, y la desventaja es la facilidad con que se puede fragmentar el cúmulo, al emplearse bloques de memoria relativamente grandes. Para evitar el problema de fragmentación del cúmulo se puede emplear una lista enlazada como la que puede verse a continuación.
Lista simplemente enlazada

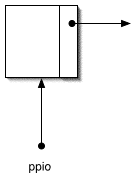
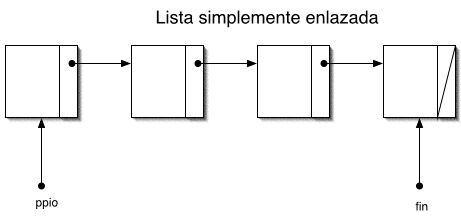
Una lista enlazada es una colección de nodos organizados de tal modo que un campo de enlace del primer nodo de la lista contiene la dirección del segundo, el campo de enlace del segundo nodo contiene la dirección del tercero, y así sucesivamente hasta llegar al último nodo de la lista. Este último nodo posee también un campo de enlace, pero el valor de ése campo es NULL, para indicar que allí finaliza la lista. En la imagen, el campo de enlace se representa como una flecha que sale del primer nodo (a la izquierda) y llega al segundo, otra flecha que sale del segundo nodo y llega al tercero, etc. El nodo final (situado en el extremo derecho) se ha representado con un campo de enlace sin flecha, cruzado por una línea diagonal.
Las listas enlazadas admiten múltiples operaciones, entre las cuales cabe mencionar las siguientes:

Adición de un nodo. Esta operación consiste en crear un nuevo nodo, dar valor a sus campos y colocar el nodo dentro de la lista, de tal modo que ésta mantenga su operatividad. La tarea es relativamente sencilla cuando se sitúa el nodo en la posición inicial o final de la lista; si es preciso hacer que ocupe una posición intermedia (por ejemplo, para mantener una lista enlazada ordenada), la inserción exige determinar previamente la dirección del nodo tras el cual situaremos el nodo nuevo.
Eliminación de un nodo. Esta operación, inversa de la anterior, consiste en tomar un nodo, proporcionar sus datos, liberar la memoria ocupada por el nodo y dejar la lista en el estado operativo habitual. Al igual que en el caso anterior, la labor más complicada es la consistente en eliminar un nodo situado en posición intermedia, esto es, un nodo que se encuentre entre dos nodos dados de la lista.
Recorrido de la lista. Esta operación consiste en acceder a todos y cada uno de los nodos de que conste la lista, aplicando posiblemente alguna operación a cada nodo. Por ejemplo, puede ser necesario recorrer una lista para mostrar en pantalla el contenido de todos sus nodos.

Para facilitar estas operaciones, es útil contar con dos punteros que señalarán siempre el primer y último nodo de la lista.El puntero de nodo inicial nos permite conocer en todo momento la dirección del primer elemento de la lista; a partir de él será posible recorrer al lista sin más que ir pasando al nodo siguiente mediante un código similar a este:

struct Nodo temp = ppio;
while (temp->sig != NULL)
	{
		printf("%d", temp->dato);
		temp = temp->sig;
	}

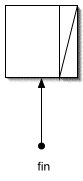
Por su parte, el puntero de nodo final marca la posición del último nodo de la lista, y permite añadir nodos al final de la lista sin recorrerla. Si no mantiene el puntero de fin de lista, será preciso determinar su posición mediante un código análogo al fragmento anterior.

struct Nodo temp = ppio;
while (temp->sig != NULL)
	{
		temp = temp->sig;
	}

En efecto, téngase en cuenta que


						temp

queda apuntando al último elemento de la lista (aquel tal que su campo de nodo siguiente tiene el valor NULL).

La utilidad de estos punteros se apreciará mejor en las próximas secciones. Ciertamente, se puede prescindir del puntero del nodo final, simplificándose en cierto modo las operaciones, pero esto tiene un coste: la adición de nodos al final de la lista pasa a ser una operación mucho más costosa que la adición de nodos al principio.

Inserción y eliminación de nodos en una lista simplemente enlazada
El problema de la inserción tiene tiene varias posibilidades relevantes, que se exponen en la tabla siguiente. Obsérvese que, finalmente, la inserción de un nodo en una lista enlazada se reduce a cuatro posibles acciones, asociadas a las operaciones de inserción al principio, inserción al final o inserción en posición intermedia.

Inserción de un nodo al principio de la lista. Es preciso considerar tres casos: que la lista esté vacía, que haya un único nodo y que haya dos o más nodos.
Inserción de un nodo al final de la lista. Es preciso considerar tres casos: que la lista esté vacía, que haya un único nodo y que haya dos o más nodos.
Inserción de un nodo entre dos nodos de la lista, buscando su posición ordenada. Es preciso considerar tres casos: que la lista esté vacía, que haya un único nodo y que haya dos o más nodos.

Visto de otra manera, la inserción de un nodo en una lista conlleva las operaciones (y tareas) siguientes, en donde los números denotan las tareas descritas después.

Tipo de lista		Operaciones de inserción
	Al principio	Al final	Ordenada
Lista vacía	1	1	1
Un único nodo	2	3	2, 3
Dos o más nodos	2	3	4

Descripción de las tareas de inserción.

Tarea 1.- Consiste en insertar un nodo en una lista vacía. Esta tarea es la misma tanto si la operación consiste en añadir el nodo al principio, al final o en posición ordenada.
Tarea 2.- Esta tarea consiste en insertar un nodo delante del primero (a su izquierda, de modo que el nodo insertado sea el nuevo primer nodo). La tarea es idéntica para el caso que haya un sólo nodo o más, y aparece tanto en listas ordenadas como en listas desordenadas.
Tarea 3.- Consiste en insertar un nodo al final de la lista, de modo que el nodo insertado sea el nuevo último nodo. La tarea es la misma si hay un nodo que si hay dos o más y aparece en listas ordenadas o desordenadas.
Tarea 4.- Consiste en insertar un nodo en posición ordenada. Sólo aparece en listas ordenadas con dos o más elementos (si hay un sólo elemento, o ninguno, la inserción de un nodo en lista ordenada se reduce a las tareas 1, 2 o 3).

En términos de estas tareas, los algoritmos de inserción en una lista enlazada pueden expresarse en la forma siguiente:

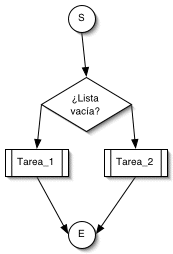
Algoritmo de inserción al principio .
Si la lista está vacía, se ejecuta Tarea_1 . Si no está vacía, se ejecuta la Tarea_2 . Internamente, añadir un nodo al principio conlleva mantener la integridad de los punteros ppio y fin . Si la lista está vacía, es preciso modificar el valor de ppio y el de fin , para hacer que el valor de ambos pase a ser la dirección del nuevo (y único) nodo. Si la lista no está vacía, entonces sólo es preciso modificar el puntero ppio , que debe tomar como valor la dirección del nuevo nodo. Por supuesto, el puntero de nodo siguiente de éste nuevo nodo debe tomar como valor la dirección del que antes fuera primer nodo. En este segundo caso, el puntero fin no resulta modificado. De aquí vienen las tareas 1 y 2 mencionadas.

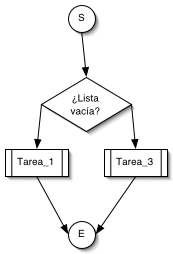
Algoritmo de inserción al final .
Si la lista está vacía, se ejecuta la Tarea_1 . Si no está vacía, se ejecuta la Tarea_3 . Internamente, añadir un nodo al final conlleva mantener la integridad de los punteros ppio y fin . Si la lista está vacía, es preciso modificar el valor de ppio y el de fin , para hacer que el valor de ambos pase a ser la dirección del nuevo (y único) nodo. Si la lista no está vacía, entonces sólo es preciso modificar el puntero fin , que debe tomar como valor la dirección del nuevo nodo. Por supuesto, el puntero de nodo siguiente del que fuera el último nodo debe tomar como valor la dirección del nuevo nodo final. En este segundo caso, el puntero ppio no resulta afectado. De aquí vienen las tareas 1 y 3 mencionadas.

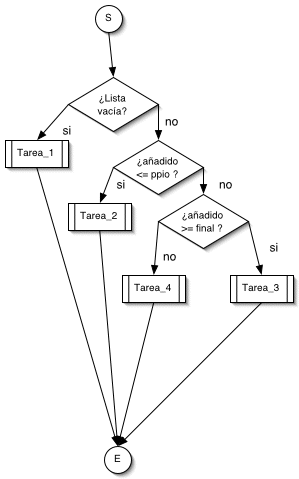
Algoritmo de inserción en posición intermedia .
Si la lista está vacía, se ejecutta Tarea_1 y hemos terminado. Si no está vacía, se comprueba si el nodo añadido es anterior al primero. Si es anterior al primero, se ejecuta la Tarea_2 y hemos terminado. Si no es anterior al primero, se comprueba si es posterior al último. Si es posterior al último, se ejecuta la Tarea_3 y hemos terminado. Si no es posterior al último (tampoco era anterior al primero), entonces se ejecuta la Tarea_4 .

La Tarea_4 se especializa en buscar la posición del nodo en listas de dos o más nodos. Una vez hallado el puntero de nodo anterior, se procede a la inserción del nodo, manteniendo siempre la integridad de la lista. Esto exige dejar la lista en un estado adecuado para que sea posible seguir añadiendo o eliminando nodos.

Téngase en cuenta que la Tarea_4 sólo llega a ejecutarse cuando hay dos o más nodos en la lista. En efecto, el primer nodo añadido dará lugar a la ejecución de la Tarea_1 exclusivamente. El segundo nodo añadido da lugar a la ejecución de Tarea_2 o de Tarea_3 , porque su valor sólo puede ser menor o igual que el almacenado en el nodo señalado por ppio , y entonces se añade delante de éste ( Tarea_2 ) o bien mayor o igual que el valor almacenado en el nodo señalado por ppio , y entonces se añadirá detrás de ppio ( Tarea_3 ). Al añadirse un tercer nodo se abre la posibilidad de ejecutar la Tarea_4 , pero únicamente a partir del tercer nodo.

El problema de la eliminación de nodos en una lista enlazada se puede abordar en dos fases: búsqueda y eliminación.

La fase de búsqueda sirve para determinar si la lista enlazada considerada contiene o no el nodo que deseamos eliminar, en función de un criterio que normalmente dependerá de los valores almacenados en el nodo. Esta fase proporciona dos informaciones como resultado:
1. La situación del nodo (al pricipio de la lista, al final o en posición intermedia).
2. El puntero necesario para eliminar el nodo en cuestión, si está en la lista.
La fase de eliminación es la encargada de liberar la memoria asociada al nodo deseado. En función de la información obtenida en la fase de búsqueda, procede a destruir el nodo.

Fase de búsqueda

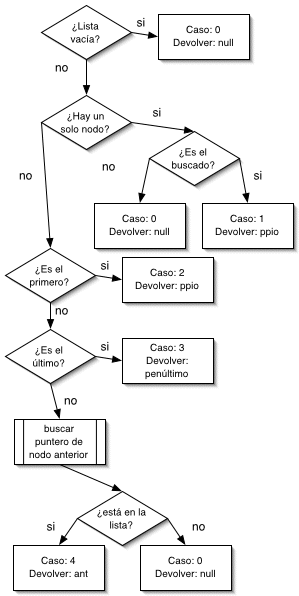El primer paso de la búsqueda consiste en determinar si la lista está vacía. De ser así, el nodo no está presente en ella; esto vamos a denominarlo Caso 0, y el puntero proporcionado será


			NULL

.

Si la lista no está vacía, se determina si hay un único nodo. Si ese único nodo es el que debe eliminarse, se denomina Caso 1 y se devuelve el puntero


			ppio

.

Si el primer y único nodo no es el buscado, se tiene de nuevo el Caso 0 y se devuelve el puntero


			NULL

.

Si no hay un sólo nodo, entonces hay dos o más. Si el nodo buscado es el primero, se denomina Caso 2 y se devuelve el puntero


			ppio

. Si el nodo buscado es el último, se denomina Caso 3 y se devuelve el puntero del penúltimo nodo.

En caso contrario tiene una lista con dos o más nodos, de la cual se sabe que el nodo buscado no es el primero ni el último. Si sólo hay dos nodos, entonces el nodo buscado no existe. Si hay tres o más nodos, se hace una búsqueda del posible nodo anterior al buscado, en que se recorre la lista con dos punteros, uno de nodo anterior (que inicialmente es igual a


			ppio

) y otro de nodo examinado (que inicialmente apunta a


			ppio->sig

, lo cual tiene sentido porque hay dos o más nodos). El recorrido se detiene cuando el nodo examinado es

fin

, o cuando el nodo examinado tiene el valor buscado. Si al finalizar el recorrido se observa que el nodo examinado tiene el valor buscado, entonces el puntero de nodo anterior nos permite efectuar la eliminación. Si no está en la lista, se tiene de nuevo el Caso 0 y se devuelve el puntero


			NULL

.

Fase de Eliminación
Una vez concluida la búsqueda, se realiza la eliminación (si procede). Es preciso estudiar los casos del 1 al 4; el Caso 0 es trivial y no es preciso hacer nada.

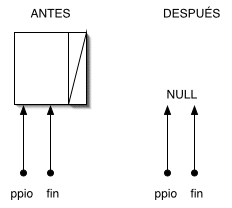
Caso 1 .- Es preciso eliminar el único nodo de la lista. Basta entonces con liberar el nodo y dar a ppio y fin el valor NULL . De esta manera la lista queda vacía y en un estado coherente; si se intenta añadir o eliminar un nodo, será posible detectar que no hay otros nodos ya existentes. Es imprescindible mantener la coherencia de la lista, dejándola siempre dispuesta para que funcione correctamente en operaciones posteriores.

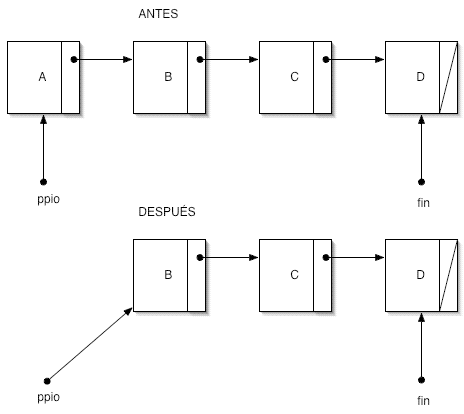
Caso 2 .- Es preciso eliminar el primer nodo de una lista con dos o más nodos. Basta hacer que ppio avance al nodo siguiente y eliminar el (viejo) nodo inicial. Téngase en cuenta la necesidad de disponer del puntero del (eliminado) primer nodo para liberar la memoria asociada al mismo. Por tanto, primero se toma nota del valor de ppio . Después, se hace que ppio pase a valer ppio->sig . Finalmente, se libera el primer nodo, de cuya dirección se ha tomado nota previamente.

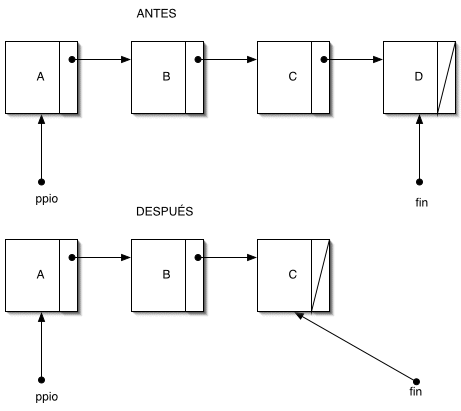
Caso 3 .- Es preciso eliminar el último nodo de una lista con dos o más nodos. Esto implica dar al puntero de nodo siguiente del penúltimo nodo el valor NULL, para mantener la integridad de la lista, y hacer que fin apunte al (nuevo) último nodo. Todo es fácil porque se nos proporciona el puntero del penúltimo nodo. La primera operación consiste en liberar la memoria asociada al último nodo, señalado por fin . La segunda consiste en hacer que el puntero fin tome como valor el del puntero del penúltimo nodo, que nos ha proporcionado la operación de búsqueda. De este modo se mantiene la integridad de la lista.

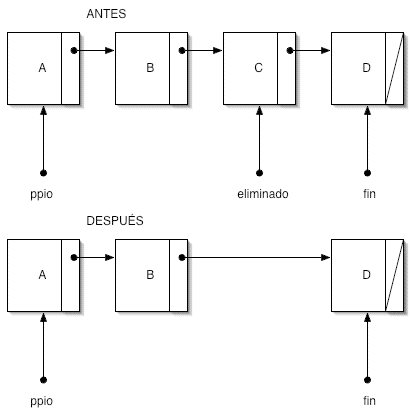
Caso 4 .- Esta consiste en hacer que el nodo anterior al eliminado (el examinado) pase a tener como nodo siguiente el nodo siguiente al eliminado. Si el nodo eliminado es el penúltimo de la lista, habrá que modificar el valor de fin , además de efectuar las operaciones habituales de eliminación. Esta eliminación es posible porque se recibe el puntero del nodo anterior al eliminado, obtenido en la fase de búsqueda. Es preciso seguir un orden de operaciones, como en el caso anterior. En primer lugar, se toma nota del puntero del nodo eliminado. A continuación, se hace que el nodo señalado por el puntero de nodo anterior tenga como nodo siguiente el nodo que sigue al eliminado. Por último, se libera la memoria del nodo eliminado.

Ejercicios propuestos

Para todos los ejercicios siguientes, las estructuras de datos empleadas como base son las siguientes:


struct Nodo {
 int dato;
 struct Nodo * sig;
};
struct Lista {
	struct Nodo *ppio, *fin;
};

Ejercicio 1103r01.- Sea una lista simplemente enlazada y basada en las estructuras anteriores. Se pide construir una función que admita como argumento un puntero de Lista y el puntero de un nodo cuyos campos ya están cumplimentados, y que realice la tarea de insertar un nodo único (tarea 1). Se supone que la lista está vacía y no es preciso comprobarlo.
Ejercicio 1103r02.- Sea una lista simplemente enlazada y basada en las estructuras anteriores. Se pide construir una función que admita como argumento un puntero de Lista y el puntero de un nodo cuyos campos ya están cumplimentados, y que realice la tarea de poner un nodo en primera posición (tarea 2). Se supone que la lista no está vacía y no es preciso comprobarlo.
Ejercicio 1103r03.- Sea una lista simplemente enlazada y basada en las estructuras anteriores. Se pide construir una función que admita como argumento un puntero de Lista y el puntero de un nodo cuyos campos ya están cumplimentados, y que realice la tarea de poner un nodo en última posición (tarea 3). Se supone que la lista no está vacía y no es preciso comprobarlo.
Ejercicio 1103r04.- Sea una lista simplemente enlazada y basada en las estructuras anteriores. Se pide construir una función que admita como argumento un puntero de Lista y el puntero de un nodo cuyos campos ya están cumplimentados, y que realice la tarea de poner un nodo en su posición ordenada dentro de la lista (tarea 4). Se supone que la lista posee dos o más nodos y no es preciso comprobarlo.
Ejercicio 1103r05.- Construir una función adecuada para buscar un nodo con el fin de eliminarlo. La función recibe como argumentos un puntero de Lista y un puntero de nodo que contiene el valor deseado. Debe proporcionar dos datos como resultado:

Una indicación de caso que seguirá la exposición anterior:
- Caso 0, el nodo buscado para su eliminación no está en la lista.
- Caso 1, es el primer nodo de la lista y hay un único nodo.
- Caso 2, es el último nodo de la lista y hay 2 o más nodos.
- Caso 3, el nodo existe y se encuentra en una posición intermedia
Y un puntero cuyo valor es el siguiente:
- Caso 0, NULL .
- Caso 1, ppio .
- Caso 2, pen , siendo pen->sig = fin .
- Caso 3, ant , siendo ant el puntero del nodo anterior al buscado para su eliminación.
Ejercicio 1103r06.- Construir una función que reciba como argumento un puntero de Lista. La función debe eliminar el primer nodo de la lista, supuesto único.
Ejercicio 1103r07.- Construir una función que reciba como argumento un puntero de Lista y un puntero, pen, que señala su penúltimo nodo. La función debe eliminar el último nodo de la lista.
Ejercicio 1103r08.- Construir una función que admita como argumento un puntero de Lista y un puntero, ant , que señala el nodo anterior al que se desea eliminar. La función debe eliminar el nodo deseado.
Ejercicio 1103r09.- Construir un programa adecuado para manejar la inserción de nodos en una lista ordenada, basado en las funciones construidas anteriormente.
Ejercicio 1103r10.- Construir un programa adecuado para manejar la eliminación de nodos en una lista ordenada, basado en las funciones construidas anteriormente.
Ejercicio 1103r11.- Construir una función que admita como argumento el nombre de un archivo de y proporcione como resultado el contenido del archivo, almacenando cada línea en un nodo de una lista enlazada. La función proporcionará su resultado mediante un puntero de Lista adecuado.
Ejercicio 1103r12.- Se dispone de un archivo binario formado por estructuras de formato conocido. Construir un programa adecuado para leer todos los nodos del archivo, almacenándolos en una lista enlazada ordenada por el campo Apellido .